K-Means & K-Medoids Clustering ^draft

The last modifications of this post were around 4 years ago, some information may be outdated!

This is a draft, the content is not complete and of poor quality!

K-Means is the most popular clustering method any learner should know. In this note, we will understand the idea of KMeans and how to use it with Scikit-learn. Besides that, we also learn about its variants (K-medois, K-modes, K-medians).

👉 Metrics for clustering methods.

K-Means

Idea?

1. Randomly choose centroids ($k$).
2. Go through each example and assign them to the nearest centroid (assign class of that centroid).
3. Move each centroid (of each class) to the average of data points having the same class with the centroid.
4. Repeat 2 and 3 until convergence.

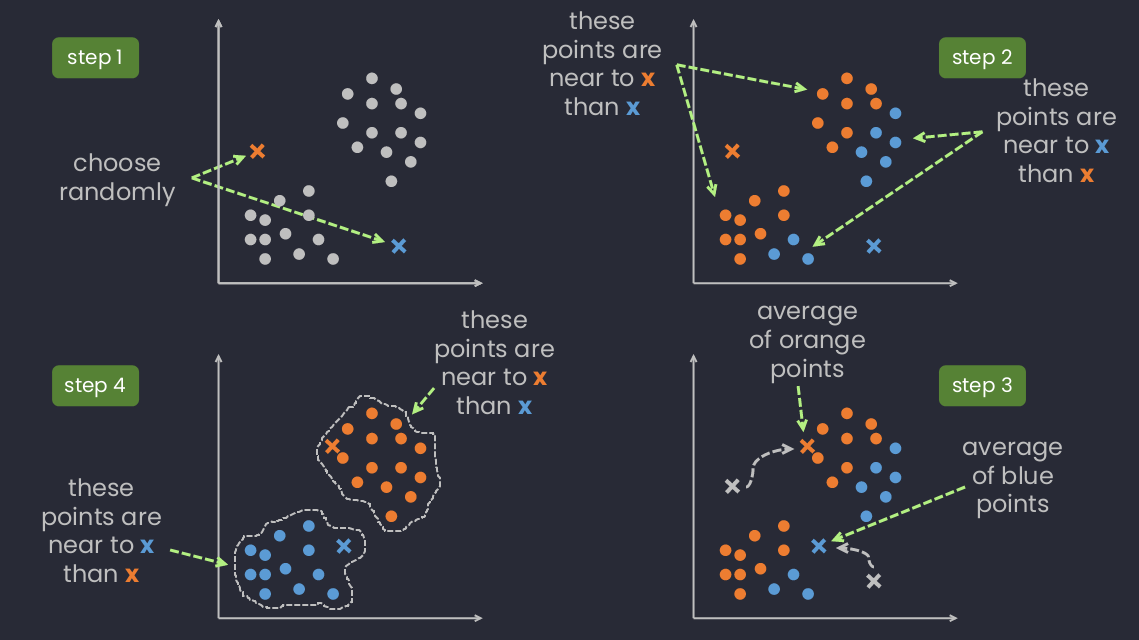
A simply basic steps of K-Means.

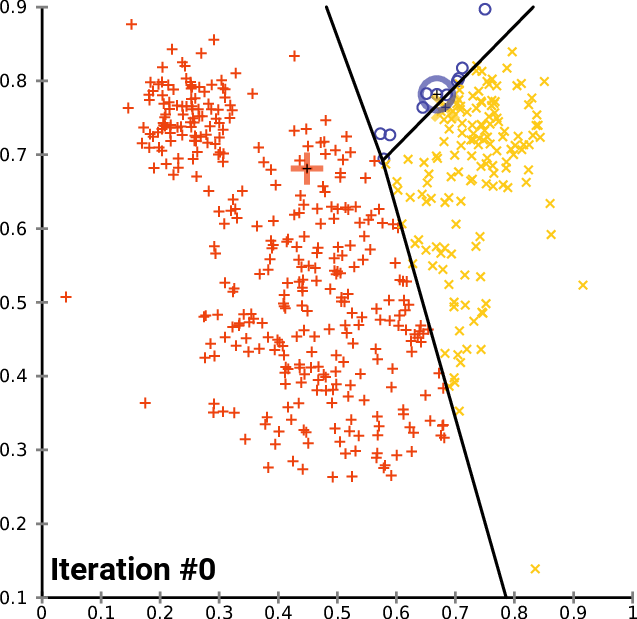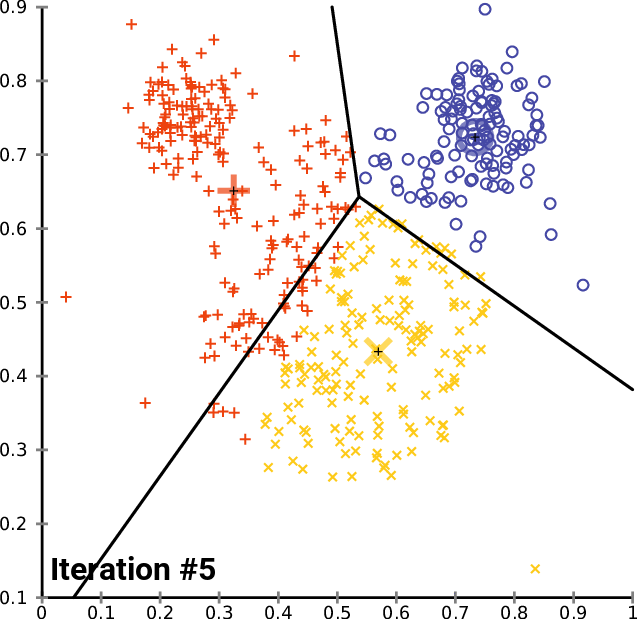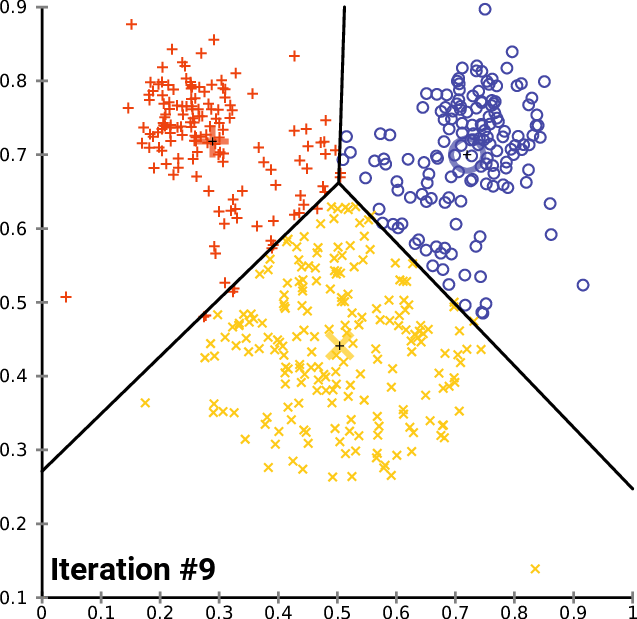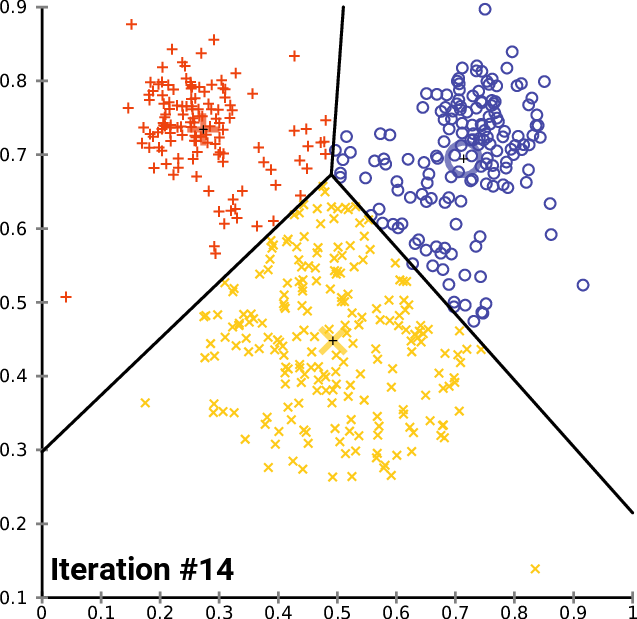
A gif illustrating the idea of K-Means algorithm. Source.

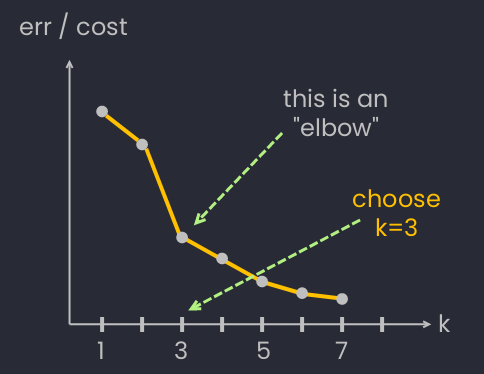
How to choose k?

Using "Elbow" method to choose the number of clusters $k$.

Discussion

• A type of Partitioning clustering.
• K-means is sensitive to outliers ⇒ K-medoids clustering or PAM (Partitioning Around Medoids) is less sensitive to outliers^[ref]

K-Means in code

from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=10, random_state=0) # default k=8

kmeans.fit(X)
kmeans.predict(X)

# or
kmeans.fit_predict(X)

Some notable parameters (see full):

• max_iter: Maximum number of iterations of the k-means algorithm for a single run.
• kmeans.labels_: show labels of each point.
• kmeans.cluster_centers_: cluster centroids.

K-Means in action

• K-Means clustering on the handwritten digits data.
• Image compression using K-Means -- Open in HTML -- Open in Colab.

K-medoids clustering

• Advantages:^[ref]
  • It is simple to understand and easy to implement.
  • K-Medoid Algorithm is fast and converges in a fixed number of steps.
  • PAM is less sensitive to outliers than other partitioning algorithms.
• Disavdvantages:^[ref]
  • The main disadvantage of K-Medoid algorithms is that it is not suitable for clustering non-spherical (arbitrary shaped) groups of objects. This is because it relies on minimizing the distances between the non-medoid objects and the medoid (the cluster centre) – briefly, it uses compactness as clustering criteria instead of connectivity.
  • It may obtain different results for different runs on the same dataset because the first k medoids are chosen randomly.
• Different from K-Means:
  • K-Means:
    • Final centers no need to be points in data.
    • Measure generally requires Euclidean distance.
    • Sensitive to outliers.
  • K-Medoids:
    • Final Centers is actual points in data. They're called medoids or exemplars.
    • Measures can be arbitrarily dissimilar.
    • Robust to outliers.

The idea:

1. (Like KMeans'): choose randomly points (no need to be a point in data)
2. (Like KMeans'): assign labels to points based on chosen points in step 1.
3. (Different from KMeans):
4. (Like KMeans'): repeat the steps.

Choose k by Silhouette

It's better than Elbow method to choose the number of clusters $k$.

👉 Check this note.

References

• Luis Serrano -- [Video] Clustering: K-means and Hierarchical.
• Andrew NG. -- My raw note of the course "Machine Learning" on Coursera.